Применение гиперкомплексных чисел

• Введение

Как известно, на данный момент достаточно активно развивается область обработки цифровых изображений. Развитие ее связано с наличием постоянного человеческого интереса к сжатию, фильтрации, распознаванию и т.д. цифровых изображений, а так же с улучшением алгоритмов обработки, осуществляющих выше указанные операции. В данной статье речь пойдет о некотором частном пересечении области обработки цифровых изображений с пространством комплексных чисел, которые играют важнейшую роль в математике, физике и других прикладных науках.

Достоверно известно, что теория комплексных чисел начала активно развиваться в первой половине 19 века французским математиком Коши Огюстен Луи (1789-1857). И, как это не странно, до наших дней она дошла практически без изменений. База применения комплексных чисел в реале может быть различной - это и радиотехника, и обработка цифровых сигналов, и анализ колебательных процессов в генераторных системах, и т.п. К тому же число классов различных комплексных чисел является достаточно большим и применять их более удобно в определенном классе задач.

В данной статье речь пойдет о классе, так называемых, гиперкомплексных (триплет или цветных) чисел, введенных в 1847 году Чарли Гревсом с целью обобщения обычных комплексных чисел на трехмерное пространство. Кратко рассмотрим их основные свойства и операции.

• Краткая теория

Данный класс чисел представим в следующем виде:

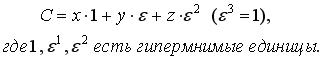Основные свойства:

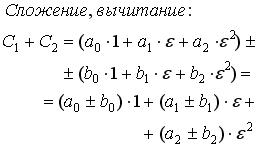
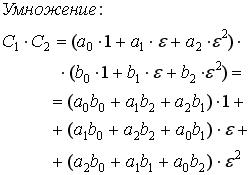
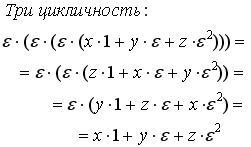Помимо этого, необходимо отметить то, что каждое гиперкомплексное число имеет три модуля, которые принимают следующий вид:

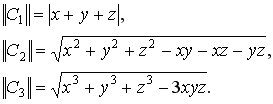Кратко рассмотрев основные свойства гиперкомплексных чисел, которые вызывают множество встречных вопросов (прежде всего в геометрической интерпретации и в свойствах гиперкомплексных единиц, не представленных здесь), необходимо обратиться к одному из применений данной математической тематики в области цифровой обработки цветных изображений.

• Применение комплексных чисел в обработке цветных изображений

Данное применение связано с задачей выделения краев изображений, которая в свою очередь прямым образом пересекается с задачей повышения резкости цифровых изображений. Классическая задача выделения краев основывается на применение дискретных лаплассиана и градиента (подробно о них можно прочитать в книге Gonzales R.C., Woods R.E. Digital Image Processing [1], выложенной на сайте http://dsp-book.narod.ru/dip_gw.htm) к цифровому изображению.

Рассмотрим наиболее подробно функцию дискретного градиента. Как известно из векторного и тензорного анализа, градиент это вектор, который характеризует (в плане цифровых изображений) направление, вдоль которого происходит изменение локальных областей интенсивности данного изображения. Поскольку градиент - это вектор, то логично предположить, что в пакетах математического моделирования, таких как Matlab, на экран монитора выводится непосредственно его модуль следующего вида:

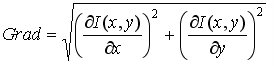или даже в линейном приближении:

В связи с этим, необходимо всегда оговаривать то, что подразумевается под функцией градиента. Если изображение представлено в градациях серого, то применяя одно из двух последних выражений, к нему можно, без особых проблем, вычислить дискретный градиент. Аналогично, можно предположить, что вычисление градиента цветного изображения (например, в модели RedGreenBlue) сводится к предварительному разделению его на цветовые компоненты, последовательному применению одного из вышеуказанных выражений для градиента к каждому цветовому каналу и, наконец, слиянию результатов трех каналов в одно изображение цветного градиента.

В некоторых случаях подобное действительно справедливо, однако, встречаются ситуации, в которых вышеприведенный алгоритм приводит к ошибкам (более или менее наглядный пример приведен в выше указанной книге). В связи с этим, разрабатываются алгоритмы решения данной проблемы. И один из таких алгоритмов как раз завязан на теории комплексного переменного, а, именно, теории гиперкомплексных чисел.

• Цветные изображения

В начале 19-го столетия Юнг предложил теорию, в которой предполагалось, что человеческая визуальная система представляет собой совокупность трех цветовых каналов: красного (Red), зеленого (Green), синего (Blue), комбинируя которые в правильных пропорциях можно получить огромную палитру цветов. В последствии, эта идея была подхвачена разработчиками и на данный момент, например, в цветных ЭЛТ мониторах PC мы имеем всем известную цветовую модель RGB.

Как оказалось, каждый цветовой пиксель модели RGB можно описать не только в виде 3-D вектора, но и в виде числа, а, именно, цветного (гиперкомплексного), введенного в краткой теории выше. Тогда в данном случае, математически, изображение представимо в виде:

• Вычисление градиента на основе стандартной матрицы Собела и гиперкомплексных чисел

Как известно, для того, чтобы вычислить проекции дискретного градиента цифрового изображения, достаточно свернуть последнее с матрицей градиента. В данном случае будет рассмотрена матрица, получившая название - градиентной матрицы Собела [1]. Вид данной матрицы для горизонтальных и вертикальных деталей, соответственно сверху вниз, представлен ниже:

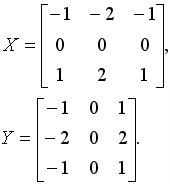Результат действия этих матриц (с использованием второй формулы для градиента) на изображение, приведенное на рис.1, представлен на рис.2.

рис.1. Исходное изображение

рис.2. Изображение, полученное при использовании матриц Собела, при последовательном применении их к Red, Green и Blue каналам

рис.3. Результат сложения Red, Green и Blue каналов изображения, представленного на рис.2

Теперь необходимо обратиться к результатам, полученным на основе теории гиперкомплексного переменного. В принципе, операция вычисления градиента основана на тех же самых формулах, которые были приведены в разделе применение комплексных чисел в обработке цветных изображений, однако, здесь нужно учитывать то, что операции вычисления модуля и умпожения (см. краткую теорию) являются отличными от тех, которые приводятся в простанстве действительного переменного. В качестве примера, приведу пару матриц, на основе которых происходило вычисление горизонтальных и вертикальных деталей, соответственно (сверху вниз) :

Результат действия этих матриц, при использовании второго выражения для градиента, дает три изображения в градациях серого. Три, потому что, как было сказано в краткой теории, каждое гиперкомплексное число имеет три модуля, а в градациях серого в силу самой операции вычисления модуля, т.к. в результате ее действия красная, зеленая и синяя компоненты изображения, полученного после действия гиперкомплексного градиента, складываются между собой. Таким образом, в результате действия гиперкомплексного градиента на изображение, пиксели которого суть гиперкомплексных чисел, получается то, что представлено на рис.4, рис.5 и рис.6.

рис.4. Гиперкомплексный градиент, вычисленный при использовании выражения для первого модуля гиперкомплексного числа

рис.5. Гиперкомплексный градиент, вычисленный при использовании выражения для второго модуля гиперкомплексного числа

рис.6. Гиперкомплексный градиент, вычисленный при использовании выражения для третьего модуля гиперкомплексного числа

Как видно из полученных результатов, вычисленный гиперкомплексный градиент на рис.4 очень схож с рис.3 и несет в себе основную информацию о контурах изображения. На рис.5 и рис.6 так же видны основные контуры, но менее четко, однако, на них хорошо видны шумы, присутствующие на изображении, в частности артефакты блочности, характерные для формата JPEG, т.к. исходное изображение имеет этот формат.

На данный момент не совсем понятно, как находить цветной гиперкомплексный градиент. Однако, вероятнее всего, его можно вычислить за счет использования первого выражения для градиента, т.к. оно сохраняет аргумент изображения. Но для осуществления данной операции нужно знать, как правильно вычислять корень из гиперкомплексного числа.